Boosting GPU Radix Sort performance: A memory-efficient extension to Onesweep with circular buffers

Radix sort is an efficient non-compare-based algorithm that can efficiently sort many discrete keys such as integers, strings, and even floating-point values. Usually, radix sort is significantly faster than compare-based algorithms when the number of sort elements is large. It distributes keys into buckets based on their individual digits and reorders them accordingly. Being a stable algorithm, this process can be repeated from the least significant digit to the most significant digit. Radix sort is also one of the most popular choices for sorting on the GPU since it can leverage compute units by splitting the input keys into GPU groups to compute them in parallel. Because of the efficiency, several applications such as spatial data structure constructions use radix sort. Thus, they can benefit from an optimized sort implementation.

Generally, GPU radix sort can be structured as follows: counting keys to build a histogram, prefix scanning to compute offsets, and reordering keys. A potential inefficiency arises when both counting and reordering read exactly the same values from the global memory multiple times, which creates redundant memory access operations. Combining kernels may resolve the redundancy, but it is not straightforward.

To address the issue, previous researchers proposed the Onesweep radix sort algorithm to reduce the number of global memory operations by combining the prefix scan and reordering stages, while minimizing the latency with the decoupled look-back method. However, since Onesweep requires a temporal buffer whose size is proportional to the number of elements to be sorted, there is still room for optimizing memory allocation.

In this article, we introduce another high-performance and memory-efficient radix sort implementation on the GPU that further improves Onesweep. Specifically, we propose an extension to reduce the allocation of temporal memory for prefix scans by using a constant-sized circular buffer. We also introduce general optimization techniques.

Before diving into Onesweep radix sort, we introduce the classic radix sort and move to Onesweep later since the algorithm is extended from the core concept. The process of the radix sort algorithm can be summarized as the following three steps: counting, prefix scan, and reordering. At the beginning of the algorithm, we count the occurrence of the elements from the given partition of input data and store the results in a bucket. Next, in order to compute the address offset of each element in the input data, we perform a prefix scan on the count result from the previous step. Since the prefix scan gives the total count of all elements that are less than an element value, the result marks the starting offset for the value. Finally, we reorder the given input data based on the calculated offset. An overview of each iteration of the sorting process is illustrated in Figure 1. Note that the bucket size used in the counting stage grows proportionally to the number of bits for sorting. For example, 32 bits for counting requires 2^{32} for the bucket size. However, since radix sort is a stable sorting algorithm, which means the relative order remains the same after being sorted for any two elements that are considered equivalent, we could partition the entire sorting process into multiple passes and start from the least-significant bit to avoid having a single gigantic bucket.

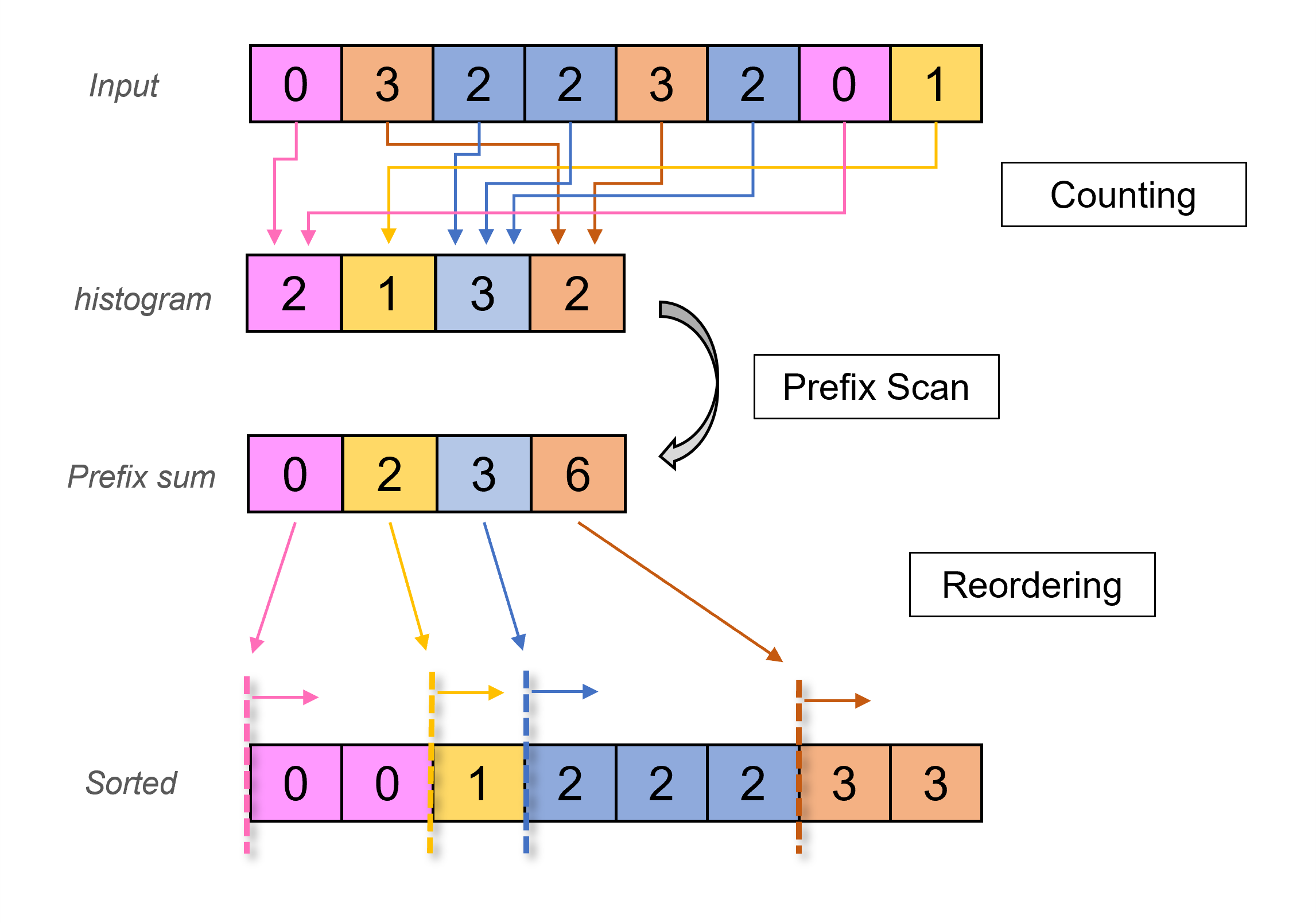Figure 1: An overview of each iteration of the standard count-scan-reorder radix sort. This example demonstrates 2-bit sorting. In counting, the bucket for each number is created to record the occurrences. The result is passed to the prefix scan to compute the global offset for each number. Finally, in reordering, those numbers are reordered based on the calculated offset and sorted accordingly.

In practice, the aforementioned three steps of classic radix sort can be implemented as individual kernels to run on GPUs. Initially, the input elements are divided into smaller chunks and assigned to GPU blocks. The output offset of each digit and each GPU block is determined in a prefix scan stage. To conduct a parallel prefix scan, the data to be processed (in this instance, the occurrences of elements stored in tables from the count) is first partitioned into chunks and allocated to individual GPU blocks. A straightforward but inefficient implementation would necessitate each GPU block to output its partial prefix sums to the global memory, followed by the launch of another kernel to merge the final result. Multi-kernel dispatches issue global barriers for synchronizing the kernels, and propagation of the partial prefix requires additional memory transfer. Consequently, this incurs a performance penalty, since kernel launch and memory transfers typically entail high latency and overhead.

One optimization method involves restructuring the prefix scan computation pattern into a single-pass kernel launch. In this pattern, the local prefix sum for each GPU block is calculated in parallel, and the global offset of each block is resolved by waiting for the preceding block to complete the local sum. Thus, this method effectively reduces the memory access for an input of n elements from 3n (with 2n reads and n writes) to 2n (with n reads and n writes) since all calculations can be done in a single kernel dispatch. This approach is known as chained scan, from a way to resolve global offsets among GPU blocks.

A performance bottleneck in classic radix sort arises from the fact that the inputs are accessed twice, once in counting and once in reordering. There is a lot of room for optimization since memory access to the global memory bears a huge latency and the read values are the same between the two kernels. Additionally, the performance of chained scan is hindered by the latency of data propagation, as each GPU block must wait for the prefix sum of its direct predecessor to become available.

In a recent development, Merrill et al. introduced a work-efficient, single-pass method for the parallel computation of prefix scan called decoupled look-back, which dramatically reduces prefix propagation latency. The key concept is to decouple the singular dependence of each GPU block on its immediate predecessor by letting the blocks access the local sums. The decoupled look-back method allows GPU blocks to inspect the status of predecessors by accumulating the local sum that is increasingly further way. On decoupled look-back, a prefix scan completion of only one of the predecessors is enough to finish looking back, while the chained-scan approach is required to wait for the direct predecessor’s prefix scan completion.

Later, Adinets and Merrill further adopted and extended this concept into the so-called Onesweep algorithm, a least significant digit (LSD) radix sorting algorithm, which further reduces the number of memory operations since it combines separated kernels into one and thus eliminates the need of accessing the same input from the global memory multiple times. Figure 2 illustrates the reordering for one particular digit in Onesweep. The prefix sum used for indicating the head of the output location for digit elements in the block is calculated on the fly by decoupled look-back. Although the reordering kernel has to pay the cost of decoupled look-back, the GPU stall is small enough compared to the chained-scan approach. Note that the output location for each digit can be calculated in advance, unlike classic radix sort, since the global histogram for each digit is invariant during the sorting process.

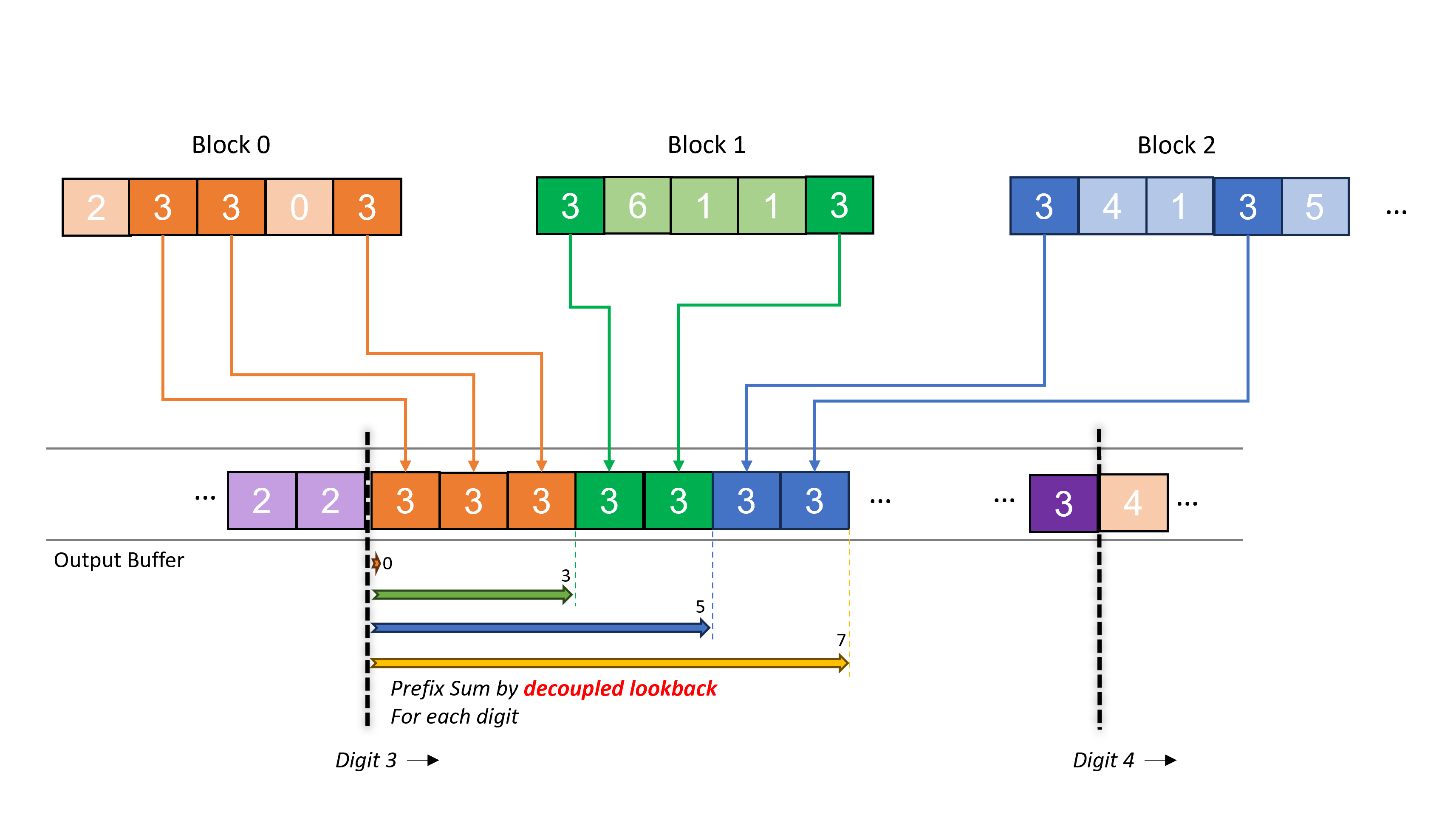
Figure 2: An illustration of reordering for a digit (3 in this example) in Onesweep. Each block first calculates a local histogram for each digit. The prefix sum for each digit is calculated by decoupled look-back and used to determine the global output location.

In decoupled look-back, each GPU block has to expose its local sum and its prefix sum later for the subsequent blocks. The status of each GPU block is initially updated through block-wise local sum computation (aggregation). Since each block’s local sum can be independently computed, the subsequent blocks can freely access the local sum of preceding blocks as soon as it becomes available. This allows them to progressively accumulate results until the complete inclusive scan (prefix sum) is achieved. Subsequently, each block’s status is further updated with its prefix sum. Practically, implementing decoupled look-back involves adding an extra status flag as a variable for each GPU block, indicating whether the local sum or prefix sum is currently available. When a block observes its predecessors, it can simply reference this status flag to determine whether it needs to accumulate the local sum or utilize the prefix sum and conclude the process. Even if the direct predecessor has not completed the calculation of the prefix scan, the local sum can be utilized instead, then the execution will attempt to read the prefix from the preceding predecessors.

Figure 3 demonstrates how decoupled look-back is performed to calculate prefix sum for the offsets. In the figure, the state transition for each block is shown in chronological order from top to bottom. Although the local sum calculation itself cannot be avoided in the looking-back process, it reduces the latency dramatically since the local sum does not have any dependency on the other blocks.

In the actual implementation, this extra status flag is packed together with the local sum and the prefix sum in a 32-bit or 64-bit structure. Customized with bitfields, the size of this structure is designed to match that of primitive types, ensuring it is treated as a primitive type when updated. This guarantees that both the content (the sum and the flag) are modified atomically in one instruction. Furthermore, we use the volatile qualifier to ensure that any reference to this variable compiles to an actual memory read or write instruction. This ensures that its effect is immediately visible to other GPU blocks and will not be cached.

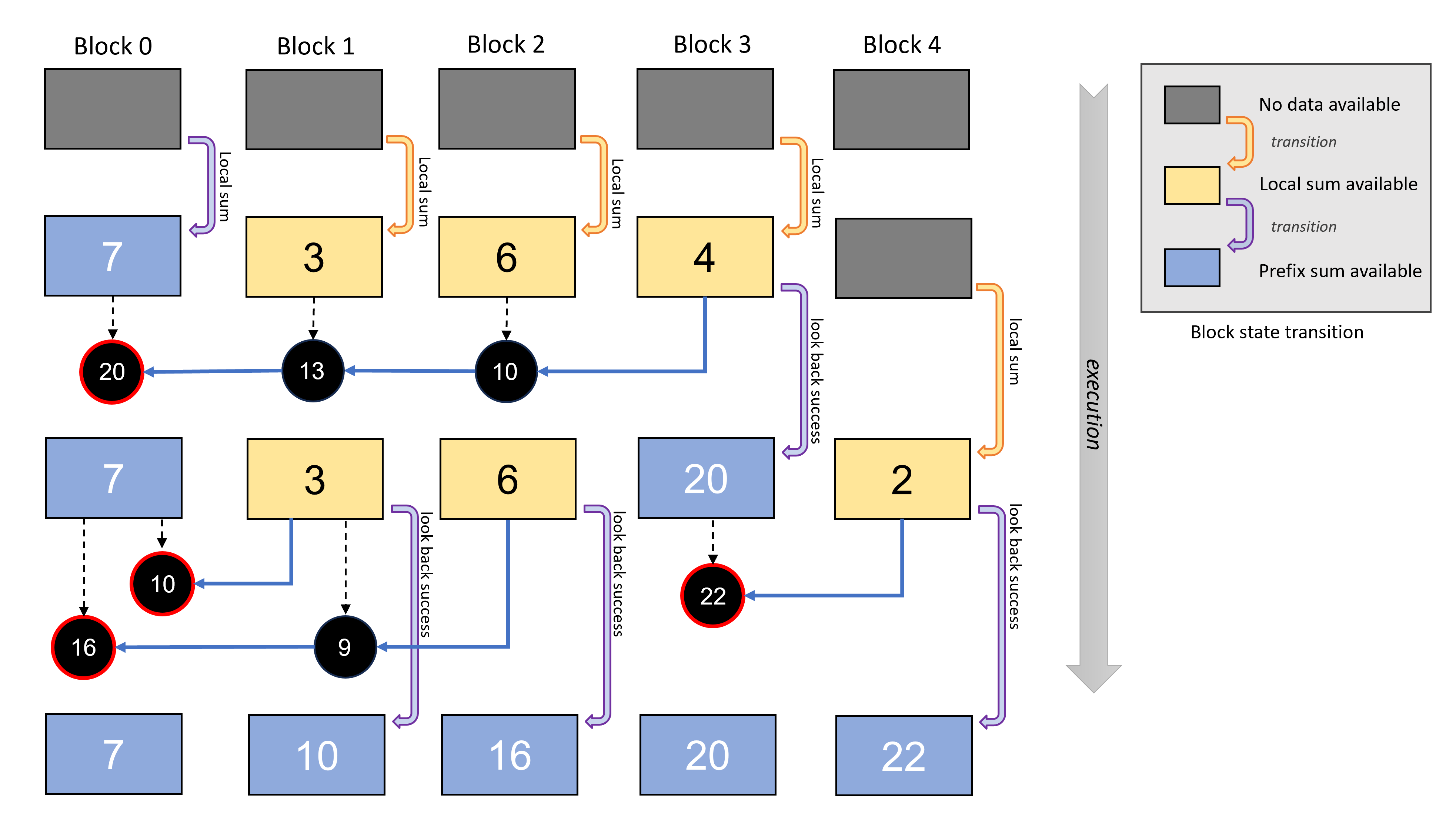
Figure 3: An example of the decoupled look-back process for prefix scan in chronological order from top to bottom. Each block checks the lower indexed blocks until the prefix sum is available (red circles) without performing spinning waits. With this look-back scheme, the prefix sum is calculated without a singular dependence and thus increases the overall efficiency.

Onesweep outperforms traditional radix sort by minimizing memory bandwidth, performing an efficient prefix scan, and having fewer kernel dispatches. Nevertheless, a drawback of the standard Onesweep lies in its requirement of temporal memory to store the status of the prefix scan for decoupled look-back, which increases proportionally with the number of elements to be sorted. This is attributed to the necessity of maintaining memory access locality and sequentiality, restricting the granularity of the chunk size per GPU block. Hence, we propose to use a circular buffer for the temporal buffer to make the allocation fixed size regardless of input elements.

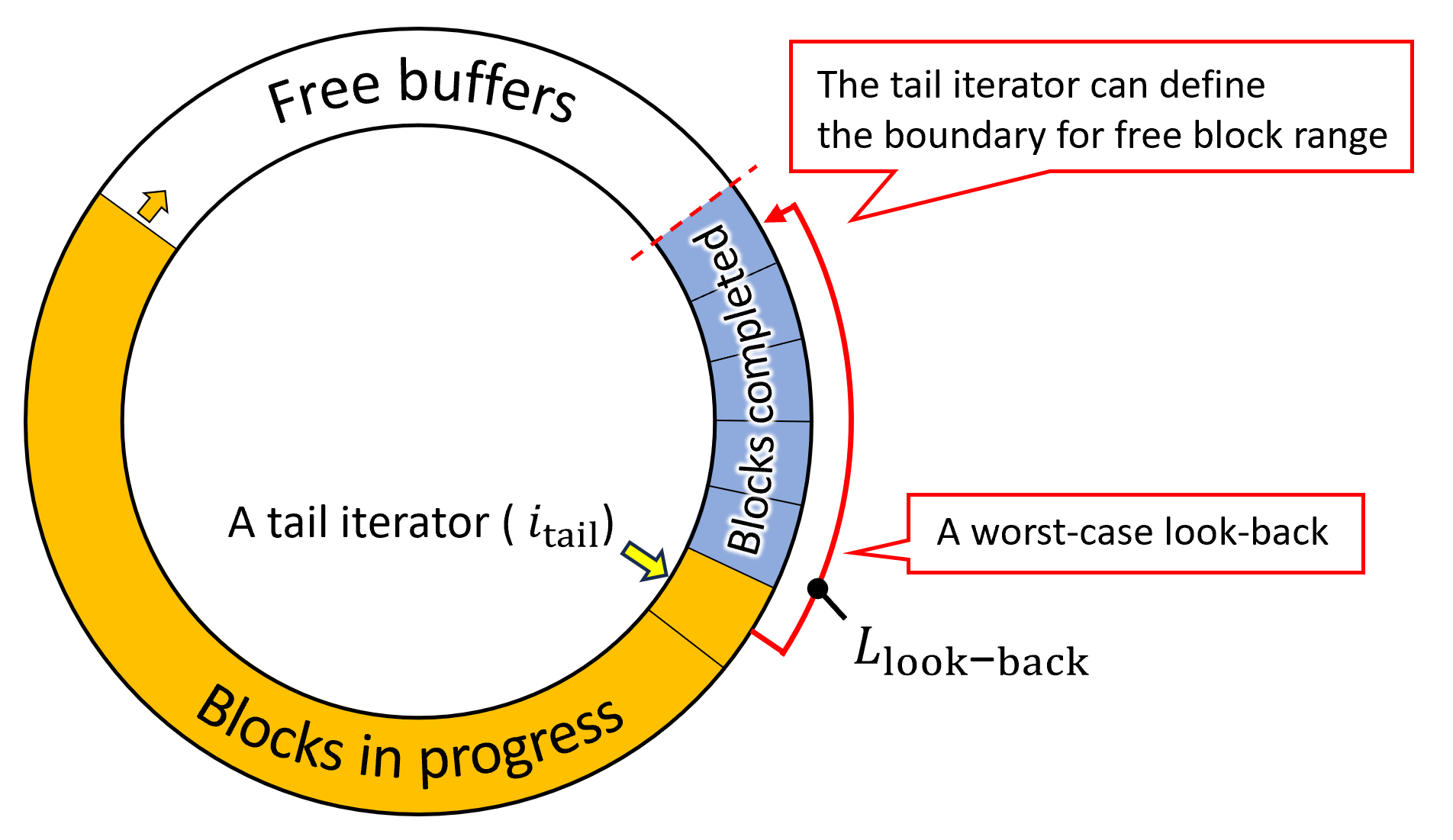
Figure 4: A circular buffer can be used for decoupled look-back. We use a tail iterator to avoid overwriting the buffers that are currently in use for looking back.

Since the standard decoupled look-back does not have a length limit for looking back, even the very last element could access the very first element theoretically. It makes the reuse of the buffer difficult. Thus, we limit the number of blocks L_lookback for looking back from the target element to make a disposable data range of the GPU blocks. Under this constraint, it is guaranteed that data in the GPU blocks that are indexed as [0, i_tail - L_lookback) are not read and can be safely overwritten in the circular buffer, where i_tail is a count of the elements that have consecutively finished processing from the first element. We call this counter a tail iterator. Figure 4 shows how the tail iterator defines the boundary of free range on a circular buffer. Note that since looking back can go beyond the tail iterator location, the boundary where we can safely overwrite is offset by L_lookback.

Listing 1 shows a naïve tail iterator increment implementation by atomic operations with sequential increments among GPU blocks. This is a serial execution of the blocks, which results in inefficient execution. Thus, we allow multiple blocks to run simultaneously to increment the iterator. This can be implemented by allowing out-of-order increments in the lowest bits to alleviate the stall. Listing 2 is the optimized tail iterator implementation. Since the higher bits are incremented sequentially, the conservative value of the tail iterator can be obtained by discarding the lower bits, where “conservative” means a buffer region of GPU blocks that is still in use is not reused. We utilise the tail iterator to wait for previous GPU blocks to avoid conflicted use of the circular buffer. The range of the GPU blocks that can use the circular buffer is [i_tail - L_lookback, i_tail - L_lookback + N_table) , where N_table is the size of the circular buffer, because the data in [0, i_tail - L_lookback ) are not read by any GPU blocks. We let decoupled look-back wait with a spin to avoid conflicts, as shown in Listing 3. Considering that the length of a look-back cannot exceed the circular buffer size, L_lookback must be smaller than N_table. As N_table has to be large enough to utilize all of the GPU processors, L_lookback < N_table is easily met.

// Listing 1: A naïve tail iterator increment. 
// The tail iterator is incremented sequentially among GPU blocks in the exact order of the index of the block.


... // Finished the use of the temporal buffer in a block. 

__syncthreads();

if( threadIdx.x == 0 )
{
    while( atomicAdd( i_tail, 0 ) != blockIdx.x )
        ;

    atomicInc( i_tail, 0xFFFFFFFF );
}

...

// Listing 2: The optimized tail iterator increment. 
// The lower bits of the tail iterator are incremented out of order to reduce spin waiting.

... // Finished the use of the temporal buffer on a decoupled 
    // lookback in a block. 

__syncthreads();

if( threadIdx.x == 0 )
{
    constexpr u32 TAIL_MASK = 0xFFFFFFFFu << TAIL_BITS;
    while( ( atomicAdd( i_tail, 0 ) & TAIL_MASK ) != ( blockIdx.x & TAIL_MASK ) )
        ;

    atomicInc( i_tail, 0xFFFFFFFF );
}

// Listing 3: A spin-waiting implementation to avoid conflicts of circular buffer use.

if( threadIdx.x == 0 && N_table <= blockIdx.x )
{
    constexpr u32 TAIL_MASK = 0xFFFFFFFFu << TAIL_BITS;
    while( ( atomicAdd( i_tail, 0 ) & TAIL_MASK ) - L_lookback + N_table <= blockIdx.x )
        ;
}
__syncthreads();

... // Decoupled look-back with a circular buffer

... // Increment tail iterator

Since the circular buffer elements are reused by multiple GPU blocks, each element has to be distinguished whether it is written by the block that is needed for the look-back. Thus, we use a 64-bit variable for each element in the table to include the block index in addition to the status flag. Despite this doubling of the allocation and that we use a conservatively large number to avoid spin waiting due to running out of the circular buffer, only 2 MB are allocated for the circular buffer in our implementation, which is negligible in practice.

The Onesweep algorithm consists of two GPU kernels: counting and reordering. In this section, we introduce optimization techniques and strategies adopted in our implementation.

In this article, we introduced advanced techniques for radix sort. We began with an overview of the classic radix sort algorithm, delved into the specifics of Onesweep radix sort, and later explored our extension aimed at optimizing temporal memory allocation and a specific look-back scheme to decouple its required size from the number of input elements. Additionally, we outlined general optimization strategies employed in our implementations. Further exploration into optimizing the sorting of smaller arrays of elements presents an intriguing avenue for future research.